线性回归

约 1994 字大约 7 分钟

machine-learning python pytorch

2024-12-21

概述

线性回归是一种基本且常用的统计和机器学习方法，主要用于揭示因变量与一个或多个自变量之间的线性关系。其主要目标是通过找到最佳拟合的线性方程来预测因变量的值。

线性回归的基本形式

单变量线性回归：只有一个自变量，模型方程为：
$y = w_1x + b$
其中 $y$ 是因变量， $x$ 是自变量， $w_1$ 是斜率（权重）， $b$ 是截距。
多元线性回归：包含多个自变量，模型方程为：
$y = w_1x_1 + w_2x_2 + \ldots + w_nx_n + b$
其中 $x_1, x_2, \ldots, x_n$ 是自变量， $w_1, w_2, \ldots, w_n$ 是各自变量的权重。

线性回归的假设

线性回归的有效性依赖于以下几个假设：

线性关系：因变量与自变量之间具有线性关系。
独立性：观测值是相互独立的。
同方差性：误差项的方差恒定。
正态性：误差项服从正态分布。

与神经网络的关系

基础模型：线性回归可以看作是神经网络的一种简单形式，尤其是在没有隐藏层和激活函数的情况下。
权重概念：在神经网络中，权重同样用于表示输入对输出的影响，并通过调整权重来学习数据模式。
扩展能力：线性回归适用于简单线性关系，而神经网络通过多层结构和非线性激活函数，可以处理更复杂的非线性关系。

应用与局限

应用：线性回归广泛用于经济学、金融学、社会科学和生物学等领域的预测和分析。
优点：模型简单、计算高效、解释性强。
缺点：受限于线性假设，无法捕捉非线性关系，对异常值敏感。

总之，线性回归是一种重要的基础工具，适用于线性关系的建模和分析。而在现代机器学习中，它也为理解更复杂的模型（如神经网络）提供了重要的理论基础。

实践

将介绍如何使用 PyTorch 框架构建一个线性回归模型，来预测笔记本电脑的价格，以及从数据加载到模型训练与评估的完整过程。

数据集

使用 Kaggle 数据集 Laptop Price Dataset，该数据集包含多种笔记本电脑的详细信息，包括品牌、型号、屏幕大小、CPU 类型、RAM 大小、重量和价格等。

导入库

导入所需的库。这些库包括用于深度学习的 PyTorch，数据处理的 Pandas，数据可视化的 Seaborn 和 Matplotlib，以及用于数据预处理和评估的 Scikit-learn。

import torch
from torch.utils.data import DataLoader, TensorDataset
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score

检查 CUDA 的可用性，以利用 GPU 加速计算：

if torch.cuda.is_available():
    print("CUDA is available! You can use GPU.")
    print("Current GPU:", torch.cuda.get_device_name(0))
else:
    print("CUDA is not available. You are using CPU.")

加载数据

通过 Pandas 加载数据集。

df = pd.read_csv('../kaggle/input/laptop-price-dataset.csv')
df.head(5)

	Company	Product	TypeName	Inches	ScreenResolution	CPU_Company	CPU_Type	CPU_Frequency (GHz)	RAM (GB)	Memory	GPU_Company	GPU_Type	OpSys	Weight (kg)	Price (Euro)
0	Apple	MacBook Pro	Ultrabook	13.3	IPS Panel Retina Display 2560x1600	Intel	Core i5	2.3	8	128GB SSD	Intel	Iris Plus Graphics 640	macOS	1.37	1339.69
1	Apple	Macbook Air	Ultrabook	13.3	1440x900	Intel	Core i5	1.8	8	128GB Flash Storage	Intel	HD Graphics 6000	macOS	1.34	898.94
2	HP	250 G6	Notebook	15.6	Full HD 1920x1080	Intel	Core i5 7200U	2.5	8	256GB SSD	Intel	HD Graphics 620	No OS	1.86	575.00
3	Apple	MacBook Pro	Ultrabook	15.4	IPS Panel Retina Display 2880x1800	Intel	Core i7	2.7	16	512GB SSD	AMD	Radeon Pro 455	macOS	1.83	2537.45
4	Apple	MacBook Pro	Ultrabook	13.3	IPS Panel Retina Display 2560x1600	Intel	Core i5	3.1	8	256GB SSD	Intel	Iris Plus Graphics 650	macOS	1.37	1803.60

检查数据集的基本信息，以确保数据完整性：

df.info()

输出

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1275 entries, 0 to 1274
Data columns (total 15 columns):
  #   Column               Non-Null Count  Dtype
---  ------               --------------  -----
  0   Company              1275 non-null   object
  1   Product              1275 non-null   object
  2   TypeName             1275 non-null   object
  3   Inches               1275 non-null   float64
  4   ScreenResolution     1275 non-null   object
  5   CPU_Company          1275 non-null   object
  6   CPU_Type             1275 non-null   object
  7   CPU_Frequency (GHz)  1275 non-null   float64
  8   RAM (GB)             1275 non-null   int64
  9   Memory               1275 non-null   object
  10  GPU_Company          1275 non-null   object
  11  GPU_Type             1275 non-null   object
  12  OpSys                1275 non-null   object
  13  Weight (kg)          1275 non-null   float64
  14  Price (Euro)         1275 non-null   float64
dtypes: float64(4), int64(1), object(10)
memory usage: 149.5+ KB

查看数据集的统计特征，以了解数据的分布情况：

df.describe()

	Inches	CPU_Frequency (GHz)	RAM (GB)	Weight (kg)	Price (Euro)
count	1275.000000	1275.000000	1275.000000	1275.000000	1275.000000
mean	15.022902	2.302980	8.440784	2.040525	1134.969059
std	1.429470	0.503846	5.097809	0.669196	700.752504
min	10.100000	0.900000	2.000000	0.690000	174.000000
25%	14.000000	2.000000	4.000000	1.500000	609.000000
50%	15.600000	2.500000	8.000000	2.040000	989.000000
75%	15.600000	2.700000	8.000000	2.310000	1496.500000
max	18.400000	3.600000	64.000000	4.700000	6099.000000

确认数据集中不存在重复记录：

df.duplicated().sum().item()

输出

数据分析

通过可视化手段，更好地理解数据中的特征关系。首先，使用热力图展示数值特征之间的相关性：

corr_matrix = df[['Inches', 'CPU_Frequency (GHz)', 'RAM (GB)', 'Weight (kg)', 'Price (Euro)']].corr()
sns.heatmap(corr_matrix, annot=True, cmap='crest', fmt=".2f", linewidths=0.5)
plt.title('Correlation Heatmap')
plt.show()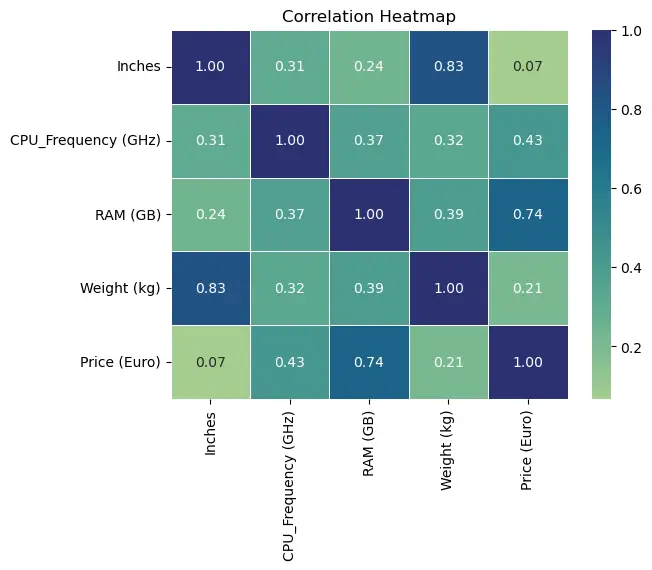

接下来，绘制成对关系图，以观察特征之间的分布和关系：

sns.pairplot(df[['Inches', 'CPU_Frequency (GHz)', 'RAM (GB)', 'Weight (kg)', 'Price (Euro)']], diag_kind='kde')
plt.suptitle('Pairplot of Numerical Features', y=1.02)
plt.show()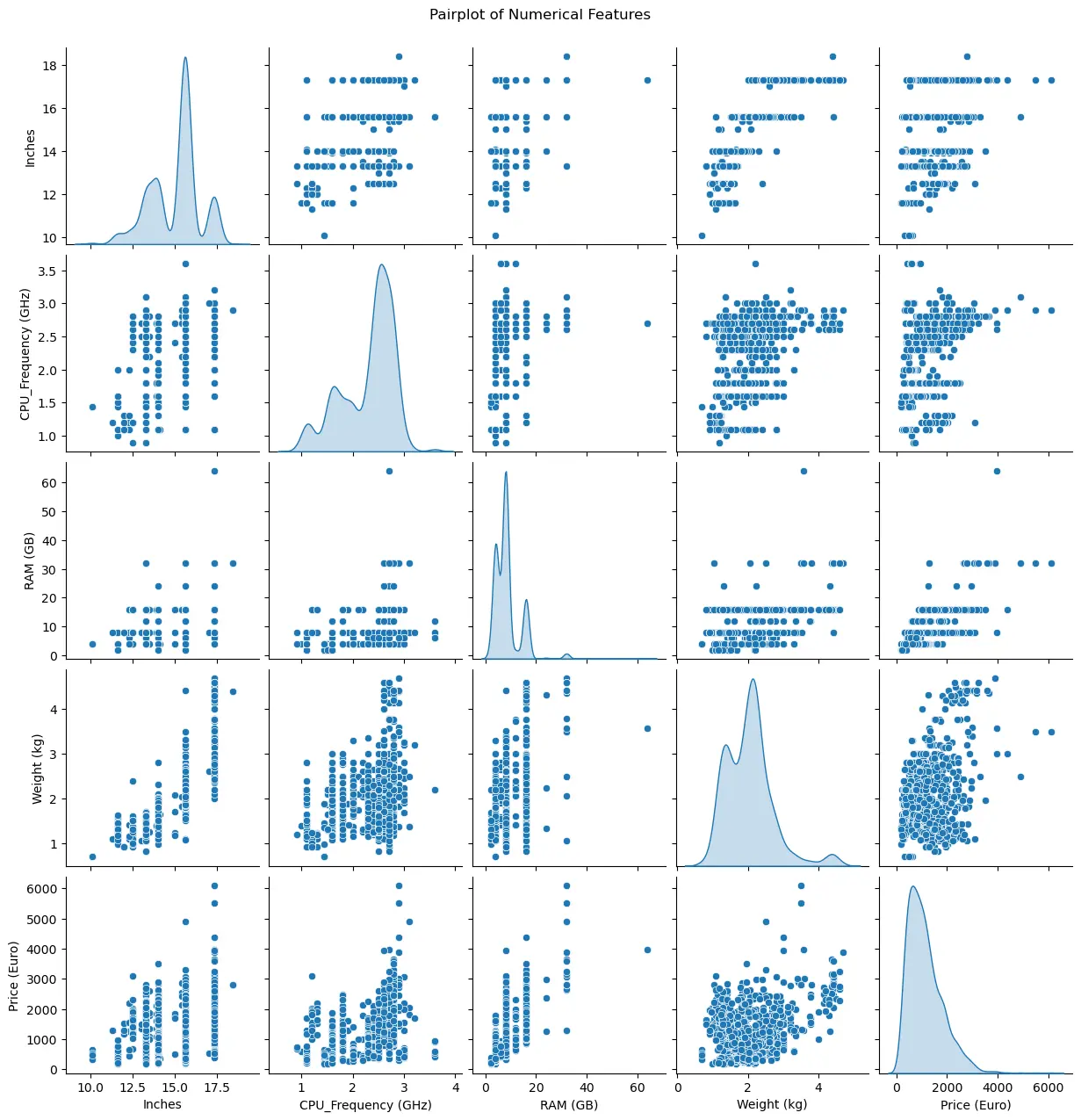

数据预处理

在数据预处理阶段，清理数据并准备特征。首先，删除 RAM 大于 60 GB 的异常值，以提高模型的准确性。

df = df[df['RAM (GB)'] <= 60]

选择特定的特征用于模型训练，并将数据集划分为训练集和测试集：

features = ['Inches', 'CPU_Frequency (GHz)', 'RAM (GB)', 'Weight (kg)']
target = 'Price (Euro)'

X = df[features].values
y = df[target].values

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

对特征和目标变量进行标准化处理，以确保模型训练的稳定性和效率：

X_scaler = StandardScaler()
X_train_scaled = X_scaler.fit_transform(X_train)
X_test_scaled = X_scaler.transform(X_test)

y_scaler = StandardScaler()
y_train_scaled = y_scaler.fit_transform(y_train.reshape(-1, 1)).flatten()
y_test_scaled = y_scaler.transform(y_test.reshape(-1, 1)).flatten()

构建和训练模型

定义一个简单的线性回归模型，使用 PyTorch 实现。线性回归模型适用于分析特征与目标变量之间的线性关系。

class LinearRegressionModel(torch.nn.Module):
    def __init__(self, input_dim):
        super(LinearRegressionModel, self).__init__()
        self.linear = torch.nn.Linear(input_dim, 1)

    def forward(self, x):
        return self.linear(x)

model = LinearRegressionModel(input_dim=len(features))

使用均方误差作为损失函数，并选择 Adam 优化器进行模型参数优化：

criterion = torch.nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)

引入学习率调度器以动态调整学习率，提高模型的训练效率：

scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode='min', factor=0.1, patience=10)

开始训练模型，每 100 个 epoch 输出一次训练损失：

num_epochs = 1000

for epoch in range(num_epochs):
    total_loss = 0
    for X_batch, y_batch in train_loader:
        y_pred = model(X_batch)
        loss = criterion(y_pred, y_batch)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        total_loss += loss.item()

    avg_loss = total_loss / len(train_loader)
    scheduler.step(avg_loss)

    if (epoch+1) % 100 == 0:
        print(f'Epoch [{epoch + 1} / {num_epochs}], Loss: {avg_loss:.4f}')

输出

Epoch [100/1000], Loss: 0.4049
Epoch [200/1000], Loss: 0.4053
Epoch [300/1000], Loss: 0.4040
Epoch [400/1000], Loss: 0.4047
Epoch [500/1000], Loss: 0.4044
Epoch [600/1000], Loss: 0.4081
Epoch [700/1000], Loss: 0.4091
Epoch [800/1000], Loss: 0.4049
Epoch [900/1000], Loss: 0.4053
Epoch [1000/1000], Loss: 0.4057

模型评估

评估模型在测试集上的表现，通过计算 MSE、RMSE、MAE 和 R² 等指标衡量模型的预测能力：

# 从模型中获取预测值
model.eval()  # 切换到评估模式
with torch.no_grad():
    y_test_pred_tensor = model(X_test_tensor)
    
# 反标准化预测结果
y_test_pred_scaled = y_test_pred_tensor.numpy().flatten()
y_test_pred = y_scaler.inverse_transform(y_test_pred_scaled.reshape(-1, 1)).flatten()

mse = mean_squared_error(y_test, y_test_pred)
rmse = root_mean_squared_error(y_test, y_test_pred)
mae = mean_absolute_error(y_test, y_test_pred)
r2 = r2_score(y_test, y_test_pred)

print(f'Mean Squared Error: {mse:.4f}')
print(f'Root Mean Squared Error: {rmse:.4f}')
print(f'Mean Absolute Error: {mae:.4f}')
print(f'R^2 Score: {r2:.4f}')

输出

Mean Squared Error: 183160.1401
Root Mean Squared Error: 427.9721
Mean Absolute Error: 310.0148
R^2 Score: 0.6527

通过散点图可视化实际价格和预测价格之间的关系，以验证模型的准确性：

plt.figure(figsize=(8, 6))
sns.scatterplot(x='Actual', y='Predicted', data=result_df, s=10)
plt.title('Actual Price vs. Predicted Price with Trendline')
plt.xlabel('Actual Price (Euro)')
plt.ylabel('Predicted Price (Euro)')
plt.plot([0, max(y_test)], [0, max(y_test)], 'b--', linewidth=1)  # 45度参考线
plt.show()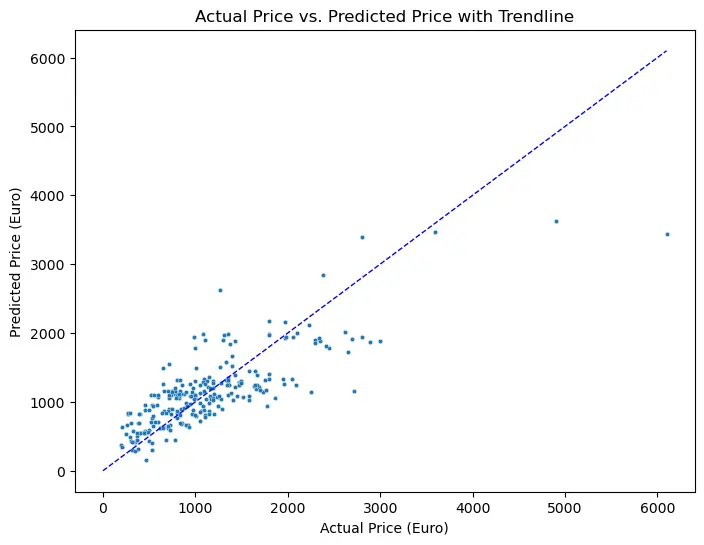

至此完成从数据导入到模型评估的全过程。

贡献者

fanwendi8

版权所有

版权归属：fanwendi8

本文链接：/machine-learning/tpmw784o/

许可证：署名-非商业性-禁止演绎 4.0 国际 (CC-BY-NC-ND-4.0)